線形回帰とは、ある予測したい値(目的変数)を別の値(説明変数)を用いて予測することです。
賃貸価格を目的変数に、物件の駅からの距離や広さを説明変数にして回帰を行うという実例があります。
本記事では、「Pythonによるあたらしいデータ分析の教科書」をベースに線形回帰モデルの作成・モデルによる予測・モデルの検証方法について学習します。
線形回帰の種類
線形回帰には2種類あります。
- 単回帰モデル—説明変数が1変数
- 重回帰モデル—説明変数が2変数以上
単回帰を計算式で表すと次のようになります。
y=ax+b
重回帰を計算式で表すと次のようになります。
y=a₀x₀+a₁x₁+a₂x₂+…+b
それぞれの回帰で求めたいのは、データの関連性を示す値(重みとも呼ばれる)a(重回帰の式であればa₀,a₁…)です。
scikit-learn を用いた線形回帰(単回帰分析)
それでは実際に線形回帰を行っていきます。
線形回帰はscikit-learnのliner_modelモジュールのLinearRegressionクラスを用いて実行します。

LinearRegressionクラスのインポート
まずは、単回帰分析を行うために必要なscikit-learnのliner_modelモジュールのLinearRegressionクラスをインポートします。
from sklearn.linear_model import LinearRegression
サンプルデータの準備
sklearnからサンプルデータをインポートします。Bostonデータセットは米国ボストンの地域別住宅価格と14個の特徴量を記録したデータセットです。
from sklearn.datasets import load_boston
boston=load_boston()
説明変数を設定
説明変数xにboston.dataを利用します。
x=boston.data

目的変数を設定
目的変数yにboston.targetを利用します。
y=boston.target
補足説明
説明変数と目的変数は次のように1行にまとめて宣言することもできます。
x,y=boston.data,boston.target
train_test_split()を用いたデータ分割
予測が正しかったかどうかを後で確認するために、データを「訓練用」と「テスト用」に分割します。分割方法はsklearnのtrain_test_splitメソッドを用います。
文字通り引数で指定した要素を2分割するための関数です。しかし、最初に下の一行を見た方は、左辺に4つも変数があってびっくりしてしまうかもしれません。これはxとyの2つの変数をそれぞれ分割して4つの変数に分けるということを1行にまとめて実行しているからなんです。
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=123)
補足説明
説明変数と目的変数を1行にまとめて宣言できたように、上のコードでも1行にまとめてそれぞれ4つの変数を宣言しているからです。つまり、上のコードは下2つのコードのように書き換えることが可能です。
from sklearn.model_selection import train_test_split
x_train,x_test=train_test_split(x,test_size=0.3,random_state=123)
from sklearn.model_selection import train_test_split
y_train,y_test=train_test_split(y,test_size=0.3,random_state=123)
train_test_split()の引数で設定できること
メソッドの引数に以下のような内容を書くことで様々な分割方法を細かく設定できます。
| test_size | 割合 | 0.0~1.0の値でテスト用のデータ(返されるリストの右側のデータセット) の割合・個数を指定。デフォルトでは25%がテスト用になる。 |
| train_size | 個数 | 0.0~1.0の値で訓練用のデータ(返されるリストの左側のデータセット) の割合・個数を指定。 |
| shuffle | 要素の並び替え | デフォルトでは要素がシャッフルされて分割される(“=True”)。 “=False”と設定すれば分割前のデータセットの順番のまま分割される。 |
| random_state | 乱数シード | シャッフル分割される場合は実行の度にランダムな分割が行われるため、 乱数シードを固定することで常に同じ分割を実行するように指定できる。 (モデルの性能を検証する時、データの分割方法によって結果が異なるため、 乱数シードを固定して同じ条件で分割させる必要がある。) |
インスタンスの呼び出し
LinearRegressionクラスのインスタンスを生成します。LinearRegressionという名前のままでは長いので、名前をlrとします。
lr=LinearRegression()
モデルの学習
モデルに学習させるために、fitメソッドを用います。引数にx,yの訓練用データを指定します。
これで説明変数xから目的変数yを求めるための式の形状をモデルに学ばせることができます。今回は単回帰なので、xとyの「訓練用データ」を用いて”直線の傾きを求める”というイメージです。
lr.fit(x_train,y_train)コード字体は1行で簡単に実行できますが、この1行でLinearRegressionクラスのインスタンスlrが直線の形状を算出してくれています。
predict()を用いたモデル予測
predict()は学習したモデルを使って予測を行います。引数にはテスト用の説明変数を渡します。そうすると、結果には予測したかった目的変数のyが返ってきます。
y_pred=lr.predict(x_test)y_predの中身を見てもらうと分かるんですが、予測結果のリストが返ってきます。
ここまでで予測自体は完了したんですが、「そもそも、作成したモデルが信頼できるのか?」という観点で、モデルの精度を検証する必要があります。
評価関数による予測モデルの検証
評価関数を算出して、予測値と本来の値の乖離具合を確認します。評価関数は様々ありますが、今回は決定係数R²を出力します。
正解値であるyの値(テスト用の目的変数データy)はy_testで、モデルの予測結果はy_pred(テスト用の説明変数データxを用いてモデルが算出した予測値)です。この2つの値の決定係数を調べることで、正解値と予測値の当てはまり具合を調べます。
当てはまりが良く乖離具合が低い時、結果は1.0に近くなります。
一方、当てはまりが悪く乖離具合が高い時、結果はマイナスに向かっていきます。
from sklearn.metrics import r2_score
r2 = r2_score(y_test,y_pred)
r2
#R2の結果
0.6485645742370706R²が64.85%でした。精度としてはまずまずでしょうか。
更に精度を高くしたい場合、通常の流れではこの後、モデルの精度を上げるために「説明変数の調整→モデル再構築→検証」の流れを繰り返し、納得がいく決定係数の値になるまでモデルの改善を行います。
予測精度の可視化
評価関数の値を確認する方法以外にも、予測値と実測値をプロットし可視化することで直感的にモデル精度を確認することもできます。
このコードでは、横軸が予測値、縦軸が実測値とする散布図をmatplotlibでプロットします。
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
ax.scatter(y_pred,y_test)
ax.plot((0,50),(0,50),linestyle='dashed',color='red')
ax.set_xlabel('predicted value')
ax.set_ylabel('actual value')
plt.show()赤い線は基準線です。y=xの直線であることから、予測値と実測値が基準線に近ければ近いほど正しい予測ができていることが直感的に分かるようになっています。
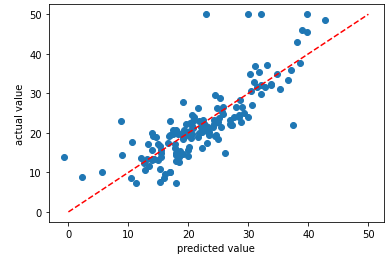
基準線から大きく外れた値もありますね。しかし、ほとんどの点が基準線に近くなっているように見えます。モデルの精度はまずまずと判断できます。
まとめ
教師あり学習の「回帰」の1つ、単回帰分析の流れである”学習用データと評価用データを分割”、”予測モデル作成”、”モデルの精度検証”を行いました。
線形回帰には、他にも説明変数が複数含まれる場合の予測を行える重回帰分析があります。
必要に応じて使い分けることで、様々なケースに対応した線形回帰を簡単に行うことができます。
参考



