本記事では学習のアウトプットとして、『Python実践データ分析100本ノック』に書かれている各ノックのコードのうち、難解と思われる部分を解説していきます。 「本に書かれている解説だけでは理解が難しい(;一_一)」と感じた方、この記事を読んで理解の一助となれば幸いです。
Python実戦データ分析100本ノックは、データの集計や分析のためのpandasや。グラフ描画に使用するmatplotlib、機械学習を行うためのscikit-learnなど、データ分析に欠かせない要素を実際に自分で手を動かしながら学ぶことができる本です。
私自身はpython初心者で、pythonを触ったことがありませんでしたが、自ら手を動かしてpythonを学習したいと思いこちらの本で学習しました。よければ手に取っていただきたいです(・ω・)ノ。
今回は第13回として、ノック61-62をやっていきます。
追記:現在第二版が2022年6月に出版されています。
本記事は第1版の内容の解説です。
第二版の解説記事もいずれ書かせていただこうと思っていますので今しばしお待ちください!
第7章 ロジスティクスネットワークの最適設計を行う10本ノック
第7章では、最適化計算を行うためのライブラリを用いて、最適化問題に取り組みます。そして、ノック51-60で学習したネットワーク可視化を実施することで、最適化計算の妥当性を確認します。
ノック61:輸送最適化問題を解いてみよう
ノック61では、ノック60までで取り組んだ輸送最適化問題を最適化計算ライブラリを用いて解きます。
ノック58でも最適化問題に取り組みましたが、最適化問題を解くには、目的関数と制約条件が必要です。そのためにpulpとortoolpyというライブラリを用いていきます。
pulpとortoolpyというライブラリは、それぞれ最適化モデル作成と目的関数の生成に使用されます。
私が普段使用している環境のcolaboratoryには、pulpとortoolpyというライブラリがないようなので、書籍には書かれていないコードですが、4行目と6行目でpipを使ってインストールしています。
エラーメッセージが表示され、書籍通りのコードで同じ場所でエラーとなった方は是非試してくださいね。
ノック61前半
import numpy as np
import pandas as pd
from itertools import product
!pip install pulp
from pulp import LpVariable, lpSum, value
!pip install ortoolpy
from ortoolpy import model_min, addvars, addvals
# データ読み込み
#trans_cost.csvは倉庫と工場の輸送コストを記載した3行(W1~W3)×4列(F1~F4)のデータです。
df_tc = pd.read_csv('trans_cost.csv', index_col='工場')
df_demand = pd.read_csv('demand.csv')
df_supply = pd.read_csv('supply.csv')
# 初期設定
#np.random.seed()関数は乱数ジェネレータを使って乱数を生成する際、乱数生成を繰り返しても同じ乱数を生成できます。
np.random.seed(1)
#trans_cost.csvのデータの内容から、nw=3です。
nw = len(df_tc.index)
#trans_cost.csvのデータの内容から、nw=4です。
nf = len(df_tc.columns)
#range関数は引数に指定した開始値から終了値までの連続した数値を要素として持つrange型のオブジェクトを作成します。
#0からカウントするため終了値はふくめません。
#今回は引数が一つなので、終了値までを指定したことになります。
#よって、range(nw)は0から2まで、range(nf)は0から3までを意味します。
#product関数で、リストの直積(デカルト積)を生成します。
#デカルト積とは、複数の値の集合から要素を一つずつとりだした組み合わせ数です。
pr = list(product(range(nw), range(nf)))
# 数理モデル作成
#「最小化を行う」モデルをm1として定義しています。これから定義する目的関数を、制約条件のもとで「最小化」できます。
m1 = model_min()
#lpSumによって、目的関数をm1に定義します。
#各輸送ルートのコストを格納したデータフレームdf_tcと最適ルートを求める主役となる変数v1とのそれぞれの要素の積の和から目的関数を定義します。
#変数v1は、LpVariableを用いてdict形式で与えます。そして、制約条件をm1に定義します。
v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}
m1 += lpSum(df_tc.iloc[i][j] * v1[i, j] for i, j in pr)
【補足説明】
コード内で書いた説明でも分かりにくいと思われる部分について、実行結果や補足説明を加えます。
pr = list(product(range(nw), range(nf)))
#やや分かりにくいので、実際の実行結果を下に示します。
#[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3)]
#LpVariableは名前の通り、変数を生成できます。
#第一引数で変数名、lowBoundで変数の下限(今回は0です)をそれぞれ指定します。
#ループ変数iとjの組み合わせをkey、それに対応する値をとしてLpVariable('v%d_%d'%(i, j)を指定して、{}で辞書内表記を作成しています。
#'v%d_%d'%(i, j)の部分ですが、書式化演算子の % を用いて、書式を新しく設定しています。%dは10進数に書式化します。
#つまり、prリストから取り出した変数iとjををv(変数i:10進数)_(変数j:10進数)という形に直しています。
v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}
#最終的なイメージは、v1={key値(i,j):v(数字i)_(数字j)}という辞書内表記を作成しています。
まだイメージしにくいので、この一行までの実行結果がこちらです。

#まず、sumではなくlpSumを使う理由ですが、高速に計算ができるからです。
#ilocを用いて倉庫と工場の輸送コストを記載したデータの各値を取り出し、その値とv1の各値の積の和を計算しています。
m1 += lpSum(df_tc.iloc[i][j] * v1[i, j] for i, j in pr)この一行までの実行結果がこちらです。
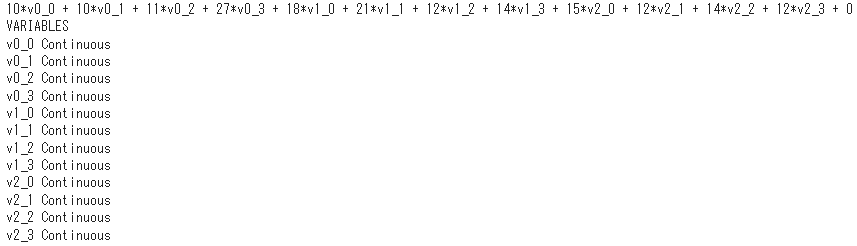
ノック61後半
#制約条件もlpSumを用いて与えます。
#ここでは『工場の製造する製品が需要量を満たす』また『倉庫の供給する部品が供給限界を超過しない』という制約条件を与えます。
for i in range(nw):
#まずはv1のkeyの片方のみを動かします。
#それによって、df_supplyのデータに書かれている各工場の製造数以下となる変数v1だけの和を計算します。
m1 += lpSum(v1[i, j] for j in range(nf)) <= df_supply.iloc[0][i]
for j in range(nf):
#次に、v1のkeyのもう片方を動かします。
#それによって、df_demandのデータに書かれている各倉庫の供給数以上となる変数v1だけの和を計算します。
m1 += lpSum(v1[i, j] for i in range(nw)) >= df_demand.iloc[0][j]
#最適化問題モデルを解きます。この時点で変数v1が最適化され、最適な輸送コストが得られます。
m1.solve()
# 総輸送コスト計算
df_tr_sol = df_tc.copy()
total_cost = 0
#v1は辞書オブジェクトであるため、要素の取り出しの際にはkeys()やitems()を使用する必要があります。
#key()は各要素のキー値
#values()は各要素の値
#items()は各要素のキー値と値のセット をそれぞれ取り出すことができます
for k, x in v1.items():
#i、jにv1のキー値(2つ)をそれぞれ格納します。
i, j = k[0], k[1]
#iとjに対応する値xを格納します。
df_tr_sol.iloc[i][j] = value(x)
#倉庫と工場の輸送コスト*x(最適化された個数)の積の和を計算しています。
total_cost += df_tc.iloc[i][j] * value(x)
print(df_tr_sol)
print('総輸送コスト:' + str(total_cost))
かなりボリューム感のあるコードでしたね。お疲れ様でした。
pulpとortoolpyというライブラリを用いて、最適化計算を行うことができました。
波括弧{}の中にキーkeyと値valueの組み合わせをkey: valueのように書くと辞書が生成される。
https://note.nkmk.me/python-dict-create/
ノック62:最適輸送ルートをネットワークで確認しよう
基本的にはノック57で解説した内容と同じでネットワークの可視化を行います。ただし、最適化計算を行ったネットワークであるため、実行結果を見ると、幾つものネットワークが存在することはなく、必要最小限のネットワークであることが分かります。
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
#データ読み込み
dt_tr=df_tr_sol.copy()
df_pos=pd.read_csv('trans_route_pos.csv')
#グラフオブジェクトの作成
G=nx.Graph()
#頂点の設定
#len(.columns)でdf_posの列(W1~W3とF1~F4まで)数7回分操作を繰り返します。
for i in range(len(df_pos.columns)):
G.add_node(df_pos.columns[i])
#辺の設定&エッジの重みのリスト化
num_pre=0
edge_weights=[]
size=0.1
for i in range(len(df_pos.columns)):
for j in range(len(df_pos.columns)):
#if notとすることで、ループ変数が同じ頂点をもつときは操作を行わないようにします。
if not (i==j):
#頂点を結び、辺の追加を行います。
G.add_edge(df_pos.columns[i].df_pos.columns[j])
#エッジの重みの追加を行います。
#1つ上のコードで追加されるedgeに対して、num_preが小さい場合if文の中の操作を行います。
if num_pre<len(G.edges):
#num_preを追加されたedge数で更新します。
num_pre=len(G.edges)
weight=0
if (df_pos.columns[i] in df_tr.columns)and(df_pos.columns[j]in df_tr.index):
if df_tr[df_pos.columns[i]][df_pos.columns[j]]:
weight=df_tr[df_pos.columns[i]][df_pos.columns[j]]*size
elif(df_pos.columns[j]in df_tr.columns)and(df_pos.columns[i]in df_tr.index):
if df_tr[df_pos.columns[j]][df_pos.columns[i]]:
weight=df_tr[df_pos.columns[j]][df_pos.columns[i]]*size
edge_weights.append(weight)
#座標の設定を行います。
pos = {}
#df_posの列(W1~W3とF1~F4まで)数7回分操作を繰り返します。
for i in range(len(df_pos.columns)):
#df_posの列(W1~W3とF1~F4まで)名をnodeという変数に格納します。
node = df_pos.columns[i]
#それぞれのnodeに対して、df_posの各行に記載されたデータを座標位置として設定します。
pos[node] = (df_pos[node][0], df_pos[node][1])
#draw()メソッドで描画します。
nx.draw(G, pos, with_labels=True, font_size=16, node_size = 1000, node_color = 'k', font_color='w', width=edge_weights)
#show()メソッドを用いて表示します。
plt.show()
輸送ルート情報のネットワーク可視化を行うことができました。
ここまでで、ノック61-62は完了です。お疲れ様でした。
今回は、輸送最適化問題を解くためのモデル作成から、最適化したネットワークの可視化までを学習できました。次回はノック63~65に取り組みます。引き続きよろしくお願いいたします。


